LovesTheTeam.com

Budete potrebovať

• Učebnica o fyzike, list papiera, ceruzka.

inštrukcia

1

Prečítajte si všeobecnú definíciu v učebnici fyzikymoment zotrvačnosti hmotného bodu vzhľadom na akýkoľvek súradnicový systém alebo iný bod. Ako je známe, toto množstvo je určené produktom hmotnosti daného materiálu materiálu štvorcom vzdialenosti od daného bodu, ktorého moment zotrvačnosti je určený, k pôvodu súradnicového systému alebo k bodu, o ktorom sa určuje moment zotrvačnosti.

2

Všimnite si, že v prípade, kdeniekoľko materiál body, moment zotrvačnosti celého systému hmotných bodov je určená v podstate rovnaké. Tak, pre výpočet momentu zotrvačnosti systému s ohľadom na nejakú súradnicovom systéme, musí súčet všetkých výrobkov hmotných bodov systému do štvorcov vzdialeností z týchto bodov na spoločnom pôvode súradnicového systému.

3

Všimnite si, že v prípade, že namiesto bodu,Ak vypočítate moment zotrvačnosti, zvážte akúkoľvek os, pravidlo na výpočet momentu zotrvačnosti sa prakticky nezmení. Jediný rozdiel je, ako sa určuje vzdialenosť od materiálových bodov systému.

4

Nakreslite čiaru na list papiera,reprezentujúce príslušnú os. Vedľa riadku na pravej a ľavej strane položte niekoľko tukových bodov, budú predstavovať materiálne body. Nakreslite kolmo z daných bodov do osi bez toho, aby sa pretína. Segmenty, ktoré získate, sú v skutočnosti normálne k osi a zodpovedajú vzdialenostiam, ktoré sa používajú na výpočet momentu zotrvačnosti vzhľadom na os. Samozrejme, vaša kresba demonštruje dvojrozmerný problém, ale v prípade trojrozmernej situácie bude riešenie podobné, ak budú kolmá na trojrozmerný priestor.

5

Pamätajte si na kurz, ktorý začal analýzu, kedyprechod od množiny diskrétnych bodov k ich nepretržitému rozdeľovaniu, je potrebné prechádzať od sumácie cez body k integrácii. To isté platí pre situáciu, keď potrebujete vypočítať moment zotrvačnosti vo vzťahu k osi tela, a nie systém bodov. V tomto prípade sa súčet bodov stáva integráciou do celého tela s intervalmi integrácie určenými hranicami tela. Hmotnosť každého bodu musí byť vyjadrená ako produkt bodovej hustoty objemovým rozdielom. Samotný diferenciál objemu je rozdelený na produkt rozdielov súradníc, pozdĺž ktorého sa uskutočňuje integrácia.

inštrukcia

1

Zvážte fyzické úloha, čo vedie k diferenciálnej rovnici, vktorý nemá argument t. Toto je problém oscilácií matematického kyvadla s hmotnosťou m zavesenou na vláknach s dĺžkou r vo vertikálnej rovine. Je potrebné nájsť pohybovú rovnicu kyvadla, ak v počiatočnom momente bolo kyvadlo stojace a odchýlilo sa od rovnovážneho stavu uhlom α. Odporové sily by mali byť zanedbané (pozri obrázok 1a).

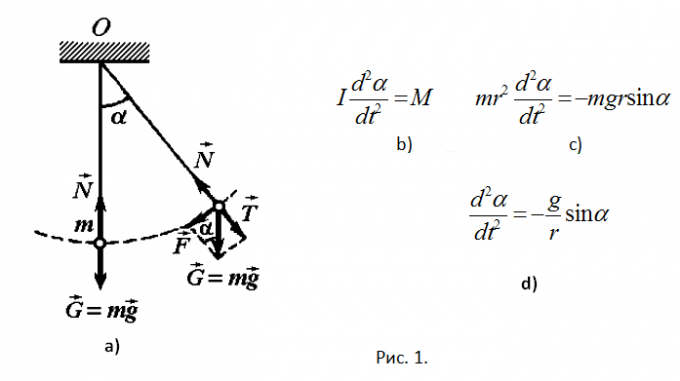
2

Riešenie. Kyvadlo je materiál bod, a suspendované v beztiaže nerozťažiteľného priadzí v bode D. Na dvoch síl: gravitácie G = mg a niť ťahová sila N. Obe tieto sily sú vo vertikálnej rovine. Preto je pre riešenie tohto problému môže byť použitie rovnice, pokiaľ ide o rotačnom pohybe okolo horizontálnej osi prechádzajúcej bodom O. Rovnica rotačného pohybu telesa má tvar znázornený na obr. 1b. Tak I - moment zotrvačnosti hmotného bodu; j - uhol natočenia závitu s bodom, merané od vertikálnej osi proti smeru hodinových ručičiek; M je moment pôsobenia síl na materiál.

3

Vypočítajte tieto množstvá. I = mr ^ 2, M = M (G) + M (N). Ale M (N) = 0, pretože jeho účinok silového vedenia prechádza bodom O. M (G) = - mgrsinj. Znak "-" znamená, že moment sily smeruje opačným smerom k pohybu. Nahradiť moment zotrvačnosti a momentu sily v rovnici pohybe a získať rovnicu zobrazené na Obr. 1c. Znížením hmotnosti vznikne vzťah (pozri obrázok 1d). Neexistuje žiadny argument t.

4

Vo všeobecnosti platí diferenciálna rovnica n-tejporiadku, ktorý nemá x a vyriešil s ohľadom na najvyšší derivát y ^ (n) = f (y, y ', y', ..., y ^ (n-1)). Pri druhom poradí je to y '' = f (y, y '). Vyriešte ju nahradením y '= z = z (y). Pretože pre komplexnú funkciu dz / dx = (dz / dy) (dy / dx), potom y '' = z'z. To vedie k rovine prvého rádu z'z = f (y, z). Vyriešte to v niektorej zo známych spôsobov a získajte z = φ (y, C1). V dôsledku toho sme získali dy / dx = φ (y, C1), ∫dy / φ (x, C1) = x + C2. Tu C1 a C2 sú ľubovoľné konštanty.

5

Konkrétne rozhodnutie závisí od typudiferenciálnej rovnice prvého rádu. Takže, ak je to rovnica s oddeliteľnými premennými, potom je riešená priamo. Ak je táto rovnica homogénna vzhľadom na y, potom pre riešenie platí substitúciu u (y) = z / y. Pre lineárnu rovnicu z = u (y) * v (y).

"Nevskaya" - to je najobľúbenejšia špirála medzirybári. Má atraktívny vzhľad a veľmi ľahko sa udržiava. Táto cievka má nízku cenu. Hmotnosť bubna je 90 g. Umožňuje umiestniť až 100 m rybárskej línie s priemerom 0,7 mm. Pomocou skrutky s poistnou maticou sa reguluje koncový výbeh. V cievke je nastaviteľný vozík. Je schopný znížiť rýchlosť otáčania bubna, aby zachránil rybára pred rozlíšením linky. Silné uťahovanie môže výrazne znížiť vzdialenosť odlievania, najlepšie je brzda bubna prstom.

"Kyjev" - cievka, ktorá je vyrobená naosi a je vybavený automatickým retardérom. Priemer vinutia je 100 mm. Buben môže držať 100 m rybárskej línie s priemerom 0,6 mm. Cievka má rohatú brzdu. Autotremóza sa odporúča používať len pri návnadách s ťažkou lyžicou a pri stredných a ľahkých návnadách sa zmenšuje vzdialenosť odlievania.

"Obolon" je zvitok vyrobený srotačný bubon o 90 °. Ak chcete, aby fungoval ako zotrvačná cievka, musíte nainštalovať bubon cez tyč. Priemer vinutia je 70 mm a je umiestnený 100 m rybárskej línie s priemerom 0,4 mm. Pre točenie je málo použiteľné, odporúča sa použiť na dno rybárskych prútov.